EM算法
主要还是跟着吴恩达的讲义(笔记)，用混合高斯分布来说明一下EM算法。
why
em算法要解决的是模型中存在隐含变量(无法在训练数据中直接观察到)的问题。
what
1.先简单说一下混合高斯分布(MoG)，MoG是一种聚类模型，说到聚类模型可能一般会先想到K-means，但如果各个类别的尺寸不同，聚类间有相关关系的时候可能MoG会更合适。直观的看如下图，
MoG包含多个正态分布，数据属于哪个正态分布可以看成一个隐含变量z。这个z符合多项式分布，
当z给定之后，x服从正态分布即条件概率p(x|z)服从正态分布，可以写出似然函数以及估计结果。
可以看到上面的计算结果里面都包含着z这个隐含变量，所以需要em算法。
2.EM(Expectation-Maximum,简称EM)算法的大致步骤是
在E-step中
上面式子算的是z的后验概率，分子是样本xi属于zj的概率，分母是样本xi属于每个zi的概率之和，因为有了参数确定的条件所以分母是个边缘分布而不是等于1。
M-step就是根据之前最大似然的结果把z的概率代入计算即可。这个过程实际上是固定z，然后最大化似然函数L(θ)求解对应的θ。
EM算法能收敛，但可能会收敛到局部最大值，如果函数是凸函数才能保证收敛到全局最大值。
这个过程用了几个技巧
(1)分子分母同时增加了Q(z)项
(2)不等号这里用到了Jensen不等式
(3)第一步和最后一步都用到了期望的定义
M-step就是根据之前最大似然的结果把z的概率代入计算即可。这个过程实际上是固定z，然后最大化似然函数L(θ)求解对应的θ。
EM算法能收敛，但可能会收敛到局部最大值，如果函数是凸函数才能保证收敛到全局最大值。
how
EM的推导过程有点长，这里只记录关键过程
这个过程用了几个技巧
(1)分子分母同时增加了Q(z)项
(2)不等号这里用到了Jensen不等式
(3)第一步和最后一步都用到了期望的定义
根据Jensen不等式等号成立的条件有
Q(z)是一个概率分布所以有∑zQi(z(i))=1，这个Q是我们自己添加的项可以这样选择Q
这个就是zi的后验概率，也就是E-step中计算的目标
所以EM算法实际上是在E-step对于当前的参数θ，找到让不等式等号成立的Q分布，在M-step对似然函数下界进行最大似然估计得到新的参数。
这个过程的图形化表示(来自从最大似然到EM算法浅解)
矩阵相关
上大学的时候线性代数学得不好很重要的一个原因是不知道线性代数在干啥，所以这里仔细的分析一下矩阵的why吧。
矩阵是什么？
矩阵表示线性变换有个前置条件“选定一组基”，完整的描述是“矩阵是线性空间中的线性变换的一个描述。在一个线性空间中，只要我们选定一组基，那么对于任何一个线性变换，都能够用一个确定的矩阵来加以描述”。
基是刻画向量空间的基本工具，n维向量空间中的n个向量如果任意其它向量都能被这n个向量线性表示，那这n个向量就是空间的基，比如最基本的是(1,0,0)，(0,1,0)，(0,0,1)这样的，但是也有其它的表示法比如(1,1,0),(1,0,1)...这样的。基可以看作线性空间的坐标系。
为了表示一个线性变换T:V-> W，我们选择V的一组基向量v1,...,vn，再选择W的一组基向量w1,...,wm，接着，把T(vk)用wk表示出来，就搞定了！就是要得到表示，
这个式子描述了V的第k个基向量被变换到W中之后的位置。
把每一个T(vk)写成基向量wi的线性组合，所需要的系数就构成了矩阵的第k列。这些是摘录自线性变换的矩阵为什么要强调在这组基下?
行列式
实际上就是线性变换的放大率，比如三维空间一个立方体经过变换以后体积变大或者变小的比率
矩阵乘法
A * B = C 两个线性变换的复合先B后A
对角化矩阵
一个线性变换T对于标准基（或者其他某个基）的矩阵为A；而我们为了更清楚地通过矩阵看出这个线性变换的效果，就把A对角化：
这个过程是先把标准基换成特征向量组成的基，然后乘上常数(对角矩阵)，再转换回标准基。
所以对角化其实就是要用一组比标准基更好的基来描述线性变换，也就是由特征向量组成的基。
矩阵相似
定义是存在可逆矩阵X满足
则我们说A和B是相似的。
矩阵相似就是同一个线性变换的不同的矩阵标识形式，之所以会有这个不同是因为两个线性变换面对的向量的基不一样。公式中X的含义是两个基之间存在线性关系能做线性变换。
则我们说A和B是相似的。矩阵相似就是同一个线性变换的不同的矩阵标识形式，之所以会有这个不同是因为两个线性变换面对的向量的基不一样。公式中X的含义是两个基之间存在线性关系能做线性变换。
逆矩阵
逆的含义是两个基下面的坐标间存在线性变换关系，也就是能变过去也能变回来。a,b是A和B的基，有b=aP，对应坐标的关系是x2=P^-1*x1。
特征值特征向量
定义，向量x与变换A满足Ax=λx，则称向量x是变换A的一个特征向量，λ是相应的特征值。
说明一个事实，A变换只是拉伸了向量x，并没有改变x的方向，所有具有相同特征值λ的特征向量加上零向量组成一个向量空间称作这个线性变换A的特征空间。
特征值是λ可以理解成拉伸程度，一个对角矩阵的特征值就是对角线上那些值，相似矩阵的特征值是相同的但特征向量一般不相同我感觉是因为基底不同。还有一层理解是因为特征向量在其它维度上是0，所以可以忽略A在其它维度上的变换所以才能等同于乘以一个常数。
特征值分解
定义，令 A 是一个 N×N 的方阵，且有 N 个线性无关的特征向量
。这样， A 可以被分解为
。这样， A 可以被分解为特征值分解的意义是寻找对该线性变换更好的表示。计算方法对于较简单的矩阵可以让|λE-A|=0然后解方程组计算，详见矩阵特征值和特征向量求解——特征值分解。对于复杂的矩阵可以用QR分解，具体见QR分解求矩阵全部特征值
SVD分解(奇异值分解)
定义，假设A是一个N * M的矩阵，将A分解成
，得到的U是一个N * N的方阵（里面的向量是正交的，U里面的向量称为左奇异向量），Σ是一个N * M的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值），V’(V的转置)是一个N * N的矩阵，里面的向量也是正交的，V里面的向量称为右奇异向量），从图片来反映几个相乘的矩阵的大小可得下面的图片，来自SVD分解技术详解
奇异值和特征值的关系，矩阵A乘以A的转置矩阵会得到一个方阵，这个方阵的特征值满足
这里的v就是右奇异向量，还可以得到
这里的σ就是上面说的奇异值，u就是上面说的左奇异向量。SVD的计算也可以通过这个关系转换成特征值分解的计算。
SVD可以用于PCA降维，这是因为在矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了，所以我们只需要保留前10%或者更少的信息就可以近似表示全部信息了。
直观理解SVD的过程，A矩阵代表的变换是从
NMF分解(非负矩阵分解)
矩阵分解还有另一种做法就是NMF分解，V≈W(权重矩阵)*H(特征矩阵) ，要求V，W，H都是非负的。
NMF可以用损失函数+梯度下降的方式来求近似解，加上正则化项如下式
最后感觉如果能多从实际意义思考一下矩阵，大学线性代数就不会学的那么差了，像线性代数的本质这样的文章就给了我很多启发。
降维
why
1.减少计算量。
2.便于数据可视化处理。
3.本质上说是提取真正有效的信息，过滤掉无用的信息。
what
降维的方法主要有因子分析模型，主成分分析(PCA)，独立成分分析(ICA)，自编码器等等。
how
1.因子分析模型
因子分析的基本目的就是用少数几个因子去描述许多指标或因素之间的联系，即将相关比较密切的几个变量归在同一类中，每一类变量就成为一个因子，以较少的几个因子反映原资料的大部分信息。
模型定义
模型假设训练数据是按下面的过程生成的，
(1)在低维空间生成m个隐变量，这m个隐变量符合多元高斯分布。
(2)用变换矩阵λ将隐含变量z由低维映射到高维。
(4)加上随机扰动即可得到最终的训练数据。
举个因子分析模型降维的实例，消费者可以通过一个24个指标构成的评价体系来评价百货商场24个方面的优劣。但消费者主要关心的是商场的环境，服务和价格，可以用因子分析法在24个维度的数据中找出环境，服务，价格的三个潜在因子，达到降维的作用。
计算过程的关键点
(1)首先要得到x的边际分布
(2)得到训练数据对应的似然函数
(3)这个似然函数很难求解，由于存在隐变量z，所以可以用em法求解。具体细节可参考
斯坦福ML公开课笔记13B-因子分析模型及其EM求解以及因子分析
2.主成分分析(PCA)
用数学的方式描述是
其中z为低维矩阵，x为高维矩阵。PCA解决的问题的一个实例是假设x代表一辆车的属性可能有最高时速，每公里耗油量等等，如果x包含了以公里为单位的最大时速和以英里为单位的最大时速，那这两个速度肯定是成比例的，x包含的信息量需要减去一个维度。PCA就是要解决去掉这样多余维度的问题。
还有一个case是飞行员的驾驶技能和对驾驶的兴趣，这两者显然是相关的，这两个属性按坐标表示如下图，
可见u1表示了两个属性的相关性，我们称之为主方向，u2则是主方向之外的噪声。
在计算寻找主方向之前，首先要对数据做预处理包括平均值归零和方差归一。
寻找主方向的过程
(1)先考虑最简化的二维空间，u是从原点出发的单位向量，每个数据点都在u方向的直线有一个投影点，寻找主方向就是想让这些投影点的方差最大化。这是因为方差最大化相当于保留了最多的信息。
(2)之所以要从原点出发是为了简化计算，这也是之前要做预处理的原因。
(3)实际情况应该是高维空间而且降维后的空间也是高维的。所以我们的做法是先找到一个主方向，再把数据集往这个主方向上投影消除掉这个主方向的影响，然后再找下一个主方向。
下面的图中，中间图投影点的方差最大。
数学表达
方差最大化可以形式化为下式最大化，
这是一个有约束
的优化问题，用拉格朗日乘子法可以得到该问题的解就是矩阵
的特征向量，最后就是一个矩阵求特征向量的问题了。详见斯坦福ML公开课笔记14——主成分分析这个问题还可以更简化，直接对训练数据的n*m的矩阵做奇异值分解，然后留下奇异值最大的r列，最终效果就是PCA想要的。如下图A矩阵的定义
因子分析法和主成分分析的区别是主成分分析仅仅做的是变量变换，而因子分析法是用假想的隐变量和随机影响变量的线性组合来表示原变量，是一种依靠概率密度的方法。主成分分析注重解释各个变量的总方差而因子分析法注重各个变量间的协方差。
还有个和PCA基本等价的概念叫流形学习，比如一个圆边界上所有的点本质上是一维的，流形学习就是学的这个映射。
3.独立成分分析(ICA)
要解决的问题是，鸡尾酒会问题：n 个人在一个 party 上同时说话，n 个麦克风放置在房间的不同位置，因为每个麦克风跟每个人的距离都不一样，所以它们记录的说话者重叠的声音也不一样。根据麦克风记录的声音，如何分离出 n 个说话者的声音呢？
问题形式化一下就是我们有x=As，x是n个麦克风采样到的声音，s是每个发言者独立发出的声音。设 W是A的逆，为一个分离矩阵，我们的目标就是找到 W，这样就能根据麦克风记录的声音 x(i)，来恢复声源 s(i)=Wx(i)。
如果A和s都是不确定的，我们无法得到精确解，因为一种情况A放大两倍s就缩小两倍，另一种情况s符合高斯分布也不行这种情况把A乘一个正交阵x变成x'结果还是满足的。
所以实际求解的时候给p(s)指定了一个密度，si的cdf需要从0到1单调递增，又不能是高斯函数所以就选择sigmoid有，
求p(x)
求似然函数
对W求导(注意这是矩阵微积分)之后得到最后的梯度下降规则。具体细节见斯坦福ML公开课笔记15—隐含语义索引、奇异值分解、独立成分分析
4.自编码器
如上图编码器对原始数据通过函数映射成一种中间标识，然后再通过解码器映射回原始数据空间，然后比较原始数据和解码的数据作为损失函数。自编码器的特点
(1)编码器和解码器一般是通过神经网络实现的
(2)自编码器是有损的
(3)自动编码器是从数据样本中自动学习的，这意味着很容易对指定类的输入训练出一种特定的编码器，而不需要做任何新工作
(4)目前自编码器的应用主要有两个方面，第一是数据去噪，第二是为进行可视化而降维。配合适当的维度和稀疏约束，自编码器可以学习到比PCA等技术更有意思的数据投影
(5)自编码器使用的神经网络可以是深度网络从而可以达到任意精度的编码
(6)自编码器有很多种，比如稀疏自编码器，去噪自编码器等等，主要的区别在于使用了不同的损失函数和正则化项
关于自编码器更多内容可以参考深度学习之自编码器AutoEncoder
5.稀疏编码
有个和降维比较类似的概念叫稀疏编码，稀疏编码的概念来自于神经生物学。生物学家提出，哺乳类动物在长期的进化中，生成了能够快速，准确，低代价地表示自然图像的视觉神经方面的能力。我们直观地可以想象，我们的眼睛每看到的一副画面都是上亿像素的，而每一副图像我们都只用很少的代价重建与存储。我们把它叫做稀疏编码，即Sparse Coding。
和pca比较类似，都是线性变换把原始数据表达成一组特征，但是pca是降维，稀疏编码的基向量的个数可能比输入的维度大，但是有稀疏性即只有少数系数远大于零学习的过程可以是拿到一副图像，然后得到一个基向量的稀疏表示。
更多详细内容可参考深度学习浅层理解（四）-- 稀疏编码
最大熵模型
why
最大熵模型是一个分类模型解决的是多分类问题。在自然语言处理里面经常见到，比如。
上面的英汉翻译中如果没有任何限制，take的七种翻译概率是相等的。但如果引入某些限制或者上下文信息，比如take后面接着一个bus那翻译成乘坐的概率就非常大。最大熵模型就是运用最大熵原理来解决这种带这某些条件或者限制的模型，这种条件或者限制称作特征函数，是个二值函数。参考最大熵模型（MaxEnt）：万法归宗（上）
what
1.最大熵原理
在已知部分知识的前提下，关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断。主要体现在(1)满足已知信息(约束条件) (2)不做任何假设(概率均等)
2.条件熵
3.最大熵模型
可以看到最大熵模型是个判别模型，唯一的约束就是x,y有某种关联f(x,y)，这个f(x,y)可以理解成x和y的亲密度的一种形式，参考如何理解最大熵模型里面的特征？
how
最大熵模型的推导详情可参考最大熵模型（MaxEnt）：万法归宗（下） 这里记录要点。
1.因为我们要得到的是p(y|x)条件分布，所以要利用最大熵原理我们需要使用条件熵。
2.利用最大熵模型我们需要优化的问题可以表示成，
把正负号反一下转换成求最小值的形式
3.由拉格朗日乘子法和对偶原理我们要求解的问题变成
要注意这里的P是个变量，是我们要求解的目标
4.对偶问题的内层极小值问题可以表示为
求L(P,w)对P(y|x)的偏导数，并让导数等于0，经过一系列代数变换就可以得到我们的最大熵模型。
5.对偶问题的外层是
用拉格朗日乘子法最初的公式表达是
P(Y|X)的对数似然函数表示为
经过一些列代数表换最后可以得到
所以有结论最大熵模型学习中的对偶函数极大化等价于最大熵模型的极大似然估计
6.有了模型如何求解呢？《统计学习方法》里面介绍了改进迭代尺度法(IIS)以及拟牛顿法。
(1)IIS基本思路还是不断更新参数让似然函数尽量大，关键是每次更新参数的尺度是通过一个方程由当前参数计算出来，细节不列了。
(2)拟牛顿法的基本思路是找一个矩阵b代替hassian矩阵，b通过b0+δ(b)的方式迭代得到，迭代公式的细节也不列了。
隐马尔科夫模型
why
隐马尔科夫模型要做的事情是“根据可观察状态的序列找到一个最可能的隐藏状态序列”，拿中文分词做例子。
中文分词，就是给一个汉语句子作为输入，以“BEMS”组成的序列串作为输出，然后再进行切词，进而得到输入句子的划分。其中，B代表该字是词语中的起始字，M代表是词语中的中间字，E代表是词语中的结束字，S则代表是单字成词。
比如下面的句子，
小明硕士毕业于中国科学院计算所
得到BEMS组成的序列为
BEBEBMEBEBMEBES
因为句尾只可能是E或者S，所以得到切词方式为
BE/BE/BME/BE/BME/BE/S
进而得到的分词结果是
小明/硕士/毕业于/中国/科学院/计算/所
这就是隐马尔科夫模型(HMM)要解决的典型的问题，我们想得到的是每个字的位置属性，但是看到的只是字本身，每个字的状态还和它之前的字的状态有关，所以我们需要根据可观察状态的序列找到一个最可能的隐藏状态序列。更详细的可以参考一个隐马尔科夫模型的应用实例：中文分词
what
1.HMM有两个重要假设，有限历史性假设和独立输出假设。如下面这张图。
(1)拿自然语言识别来看，一个词发生的概率应该是之前所有词发生情况下的条件概率但是马尔科夫链做了简化可以只算这个词前面那个词发生情况下的条件概率。状态转移的概率只依赖前一个状态。
(2)独立输出假设是说第 i 时刻的接收信号 oi 只由发送信号 si 决定。
2.HMM 有5个要素。
观测序列－O：小明硕士毕业于中国科学院计算所
状态序列－S：BEBEBMEBEBMEBES
初始状态概率向量－π：句子的第一个字属于{B,E,M,S}这四种状态的概率
状态转移概率矩阵－A：如果前一个字位置是B，那么后一个字位置为BEMS的概率各是多少
观测概率矩阵－B：在状态B的条件下，观察值为耀的概率，取对数后是-10.460
3.HMM需要解决的问题有3类
(1)似然度(概率计算)问题：参数(O，π，A，B)已知的情况下，求(π，A，B)下观测序列O出现的概率。(Forward-backward算法)。这里O已知是指我们已经得到了一个观测序列O={o1,o2...ot}。
(2)解码(预测)问题：参数(O，π，A，B)已知的情况下，求解状态值序列S。(viterbi算法)
(3)学习问题：参数(O)已知的情况下，求解(π，A，B)。(Baum-Welch算法)
4.需要注意HMM是个生成模型，对状态序列分布本身p(x)和给定状态之后的观测值p(y|x)都进行了建模。
how
1.概率计算问题，直观的做法是列举所有可能出现长度为T的状态序列，然后计算对应的概率再求和得到观察序列的概率，但是复杂度是指数级所以不可行。
前向算法是个动态规划算法，关键是建立递推关系
后向算法类似，可以参考《统计学习方法》
2.解码问题是要求t时刻最可能出现的状态i，是个最优路径问题，所以也可以用动态规划算法(viterbi算法)求解，关键是建立递推关系
3.HMM的训练可以用最大似然来做，需要训练数据由大量长度相同的观测序列和状态序列组成{(O1,I1),(O2,I2),...(Os,Is)}。但这种方法人工标注成本太高，所以一般会用非监督学习的Baum-Welch算法来搞。
当训练数据只有观测序列{O1,O2...Os}的时候我们可以把状态序列看做隐变量，那隐马尔科夫模型就变成了含隐变量的模型
这样就可以用EM算法来求解了，细节参考《统计学习方法》
条件随机场
why
首先条件随机场(CRF)的应用和HMM类似，也是解决自然语言识别中的各种词性标注，分词这些问题。但是HMM的两个假设过强，使得当前位置的词（观测）只可以利用当前的状态（词性），当前位置的状态又只能利用上一位置的状态，所以模型必要会丢掉不少信息。而CRF 的特征函数中，输入包含 (yi-1,yi,x,i) ，对于当前位置 i 来说可以利用完整的 x 信息，所以CRF可以表现得更优秀。NLP —— 图模型（二）条件随机场（Conditional random field，CRF）这篇文章里面有更详细的比较。
条件随机场这个名字听着很玄，来解读一下。
(1)随机场是由若干个位置组成的整体，当给每一个位置中按照某种分布随机赋予一个值之后，其全体就叫做随机场。还是举词性标注的例子：假如我们有一个十个词形成的句子需要做词性标注。这十个词每个词的词性可以在我们已知的词性集合（名词，动词...)中去选择。当我们为每个词选择完词性后，这就形成了一个随机场。
(2)马尔科夫随机场是随机场的特例，它假设随机场中某一个位置的赋值仅仅与和它相邻的位置的赋值有关，和与其不相邻的位置的赋值无关。继续举十个词的句子词性标注的例子： 如果我们假设所有词的词性只和它相邻的词的词性有关时，这个随机场就特化成一个马尔科夫随机场。比如第三个词的词性除了与自己本身的位置有关外，只与第二个词和第四个词的词性有关。
(3)CRF是马尔科夫随机场的特例，它假设马尔科夫随机场中只有X和Y两种变量，X一般是给定的，而Y一般是在给定X的条件下我们的输出。这样马尔科夫随机场就特化成了条件随机场。在我们十个词的句子词性标注的例子中，X是词，Y是词性。因此，如果我们假设它是一个马尔科夫随机场，那么它也就是一个CRF。设X与Y是随机变量，P(Y|X)是给定X时Y的条件概率分布，若随机变量Y构成的是一个马尔科夫随机场，则称条件概率分布P(Y|X)是条件随机场。
更详细的解读请看条件随机场CRF(一)从随机场到线性链条件随机场
条件随机场这个名字听着很玄，来解读一下。
(1)随机场是由若干个位置组成的整体，当给每一个位置中按照某种分布随机赋予一个值之后，其全体就叫做随机场。还是举词性标注的例子：假如我们有一个十个词形成的句子需要做词性标注。这十个词每个词的词性可以在我们已知的词性集合（名词，动词...)中去选择。当我们为每个词选择完词性后，这就形成了一个随机场。
(2)马尔科夫随机场是随机场的特例，它假设随机场中某一个位置的赋值仅仅与和它相邻的位置的赋值有关，和与其不相邻的位置的赋值无关。继续举十个词的句子词性标注的例子： 如果我们假设所有词的词性只和它相邻的词的词性有关时，这个随机场就特化成一个马尔科夫随机场。比如第三个词的词性除了与自己本身的位置有关外，只与第二个词和第四个词的词性有关。
(3)CRF是马尔科夫随机场的特例，它假设马尔科夫随机场中只有X和Y两种变量，X一般是给定的，而Y一般是在给定X的条件下我们的输出。这样马尔科夫随机场就特化成了条件随机场。在我们十个词的句子词性标注的例子中，X是词，Y是词性。因此，如果我们假设它是一个马尔科夫随机场，那么它也就是一个CRF。设X与Y是随机变量，P(Y|X)是给定X时Y的条件概率分布，若随机变量Y构成的是一个马尔科夫随机场，则称条件概率分布P(Y|X)是条件随机场。
更详细的解读请看条件随机场CRF(一)从随机场到线性链条件随机场
what
1.演变
CRF是马尔科夫随机场的特例，马尔科夫随机场是概率无向图模型，其定义为，设有联合概率分布 P(V) 由无向图 G=(V, E) 表示，图 G 中的节点表示随机变量，边表示随机变量间的依赖关系。如果联合概率分布 P(V) 满足成对、局部或全局马尔可夫性，就称此联合概率分布为概率无向图模型或马尔可夫随机场。
成对，局部，全局马尔科夫性理解比较简单，主要就独立性，整体的联合分布能拆解成部分概率的乘积，详见NLP —— 图模型（二）条件随机场（Conditional random field，CRF）
有了马尔科夫性就可以做无向图的因子分解，给定无向图 G ，其最大团为 C ，那么联合概率分布 P(Y) 可以写作图中所有最大团 C 上的势函数（potential function） ψC(YC) 的乘积形式：
加入条件概率分布模型 P(Y|X)的马尔科夫随机场就演变成CRF，我们关注的是线性链条件随机场（linear chain conditional CRF），是由输入序列来预测输出序列的判别式模型。
2.定义
条件随机场正式的定义是，如果随机变量 Y 构成一个由无向图 G=(V, E) 表示的马尔可夫随机场，对任意节点 v∈V 都成立，即
P(Yv|X,Yw,w≠v)=P(Yv|X,Yw,w∼v)
对任意节点 v 都成立，则称 P(Y|X) 是条件随机场。式中 w≠v 表示 w 是除 v 以外的所有节点，w∼v 表示 w 是与 v 相连接的所有节点。
线性链条件随机场的定义为
P(Yi|X,Y1,...,Yi−1,Yi+1,...,Yn)=P(Yi|X,Yi−1,Yi+1),i=1,...,n
其中当 i 取 1 或 n 时只考虑单边。
3.参数化形式
给定一个线性链条件随机场 P(Y|X) ，当观测序列为 x=x1x2⋯ 时，状态序列为 y=y1y2⋯ 的概率可写为
上面的式子中有两个特征函数，
转移特征 tk(yi−1,yi,x,i) 是定义在边上的特征函数（transition），依赖于当前位置 i 和前一位置 i-1 ；对应的权值为 λk 。
状态特征 sl(yi,x,i) 是定义在节点上的特征函数（state），依赖于当前位置 i ；对应的权值为 μl 。
一般来说，特征函数的取值为 1 或 0 ，当满足规定好的特征条件时取值为 1 ，否则为 0 。
k和l个人理解是超参数，和状态数以及y的取值没有直接关联。
特征函数的实例可以看概率图模型体系：HMM、MEMM、CRF，从特征函数可以看到CRF比HMM强大的地方在于 CRF 的特征函数中，输入包含 (yi−1,yi,x,i) ，对于当前位置 i 来说可以利用完整的 x 信息。
4.简化形式
用统一的形式表达转移函数t和状态函数s，可以得到简化形式
5.矩阵形式
矩阵表达方式和参数化形式等价，矩阵行索引是上一个状态的所有可能取值，矩阵列索引是当前状态的所有可能取值。
要注意的点一个是α是个非规范化概率和我们要求的p(y|x)差着归一化常量，第二是α是个向量，在标记问题中如果有m种标记，yi就可能有m种取值那αi(x)就是个m维向量。
另外我们还要有归一化因子，对应着α(yi)的m个值的求和。
利用前向向量和后向向量可以得到
条件随机场正式的定义是，如果随机变量 Y 构成一个由无向图 G=(V, E) 表示的马尔可夫随机场，对任意节点 v∈V 都成立，即
P(Yv|X,Yw,w≠v)=P(Yv|X,Yw,w∼v)
对任意节点 v 都成立，则称 P(Y|X) 是条件随机场。式中 w≠v 表示 w 是除 v 以外的所有节点，w∼v 表示 w 是与 v 相连接的所有节点。
线性链条件随机场的定义为
P(Yi|X,Y1,...,Yi−1,Yi+1,...,Yn)=P(Yi|X,Yi−1,Yi+1),i=1,...,n
其中当 i 取 1 或 n 时只考虑单边。
3.参数化形式
给定一个线性链条件随机场 P(Y|X) ，当观测序列为 x=x1x2⋯ 时，状态序列为 y=y1y2⋯ 的概率可写为
上面的式子中有两个特征函数，
转移特征 tk(yi−1,yi,x,i) 是定义在边上的特征函数（transition），依赖于当前位置 i 和前一位置 i-1 ；对应的权值为 λk 。
状态特征 sl(yi,x,i) 是定义在节点上的特征函数（state），依赖于当前位置 i ；对应的权值为 μl 。
一般来说，特征函数的取值为 1 或 0 ，当满足规定好的特征条件时取值为 1 ，否则为 0 。
k和l个人理解是超参数，和状态数以及y的取值没有直接关联。
特征函数的实例可以看概率图模型体系：HMM、MEMM、CRF，从特征函数可以看到CRF比HMM强大的地方在于 CRF 的特征函数中，输入包含 (yi−1,yi,x,i) ，对于当前位置 i 来说可以利用完整的 x 信息。
4.简化形式
用统一的形式表达转移函数t和状态函数s，可以得到简化形式
5.矩阵形式
矩阵表达方式和参数化形式等价，矩阵行索引是上一个状态的所有可能取值，矩阵列索引是当前状态的所有可能取值。
how
CRF的计算和HMM一样也是要解决3个问题，概率计算问题，解码问题和学习训练问题。
1.概率计算
使用的是和HMM类似的前向后向算法，定义了前向向量α和后向向量β
·
要注意的点一个是α是个非规范化概率和我们要求的p(y|x)差着归一化常量，第二是α是个向量，在标记问题中如果有m种标记，yi就可能有m种取值那αi(x)就是个m维向量。
另外我们还要有归一化因子，对应着α(yi)的m个值的求和。
利用前向向量和后向向量可以得到
2.解码
同样是用维特比算法求解，关键在于建立递推公式
δi(l),表示在位置i标记l各个可能取值(1,2...m)对应的非规范化概率的最大值，局部状态Ψi+1(l)来记录使δi+1(l)达到最大的位置i的标记取值。
3.学习训练
先得到似然函数
同样是用维特比算法求解，关键在于建立递推公式
δi(l),表示在位置i标记l各个可能取值(1,2...m)对应的非规范化概率的最大值，局部状态Ψi+1(l)来记录使δi+1(l)达到最大的位置i的标记取值。
3.学习训练
先得到似然函数
然后对w求导，通过梯度下降或者IIS以及拟牛顿法求解。
4.YY一下，crf的条件概率公式虽然和最大熵模型很像，但实际上是通过独立最大团假设的过程推导过来的。两个公式虽然很像，但实际上crf有两层，外层求和是n个状态，内层求和是k个特征函数，所以实际上是不一样的。但是简化的crf概率公式由于是n个状态求和，也可以看做是整体y的状态，这样就只有k个特征公式，这样就可以按最大熵模型的方式去看了。
决策树和随机森林
相对简单一些就不用why-what-how来分析了。
1.决策树是一个分类模型，其优点是分类路径很清晰。
2.决策树构建，用每一列的每一种取值可能来对集合做一个划分，然后比较所有划分方式的熵减少。取到熵减少最多的把集合划成两拨，然后递归这个过程。
3.随机森林，进行决策树划分的时候不是取所有属性的最优而是随机取k个属性然后在这k个属性中取最优，重复m次形成m颗树，然后m颗树加权做出决策。
4.随机森林是一种bagging的做法，也就是用多次采样的数据训练多个不同的算法然后叠加生成结论。这种是可以并行的。
3.随机森林，进行决策树划分的时候不是取所有属性的最优而是随机取k个属性然后在这k个属性中取最优，重复m次形成m颗树，然后m颗树加权做出决策。
4.随机森林是一种bagging的做法，也就是用多次采样的数据训练多个不同的算法然后叠加生成结论。这种是可以并行的。
Boost方法
why
Boosting算法是将“弱学习算法“提升为“强学习算法”的过程，主要思想是“三个臭皮匠顶个诸葛亮”。一般来说，找到弱学习算法要相对容易一些，然后通过反复学习得到一系列弱分类器，组合这些弱分类器得到一个强分类器。更详细的参考AdaBoost原理详解
what
常见的boost方法有AdaBoost，GBDT，XGBoost等等。
how
1.AdaBoost详细见AdaBoost原理详解
(1)基本原理是用比较简单的分类算法比如逻辑回归或者单层决策树去组合成比较复杂的分类算法，组合的方式就是用加权求和。
(2)训练的过程是首先给每个样本一个默认权值，然后用最简单的分类器去得到一个最佳分类，最佳分类的损失函数就是分错类的样本的权值和。
(3)分类器的权值是损失值的一个log函数，这个log函数很容易用损失函数求导获得，然后更新每个训练样本的权值，训练样本的权值是个指数函数。
(4)每轮迭代用最后的加权函数做分类，如果效果足够好就结束。
(1)GBDT是前向分布算法用多颗树组成最终的算法
(2)第m次迭代我们需要优化的损失函数如下
(3)如果我们用平方误差作为损失函数，就可以得到对残差r进行拟合的形式
(4)对于多数损失函数不太适合残差的方式，可以用损失函数的负梯度来拟合。第m次迭代时，计算当前要拟合的残差rmi。
以rmi为输出值，对rmi拟合一个回归树（此时只是确定了树的结构，但是还未确定叶子节点中的输出值），然后通过最小化当前的损失函数，并求得每个叶子节点中的输出值cmj，j表示第j个叶子节点
更新当前的模型fm(x)为：
(5)最终的模型，其中M表示基学习器的个数，J表示叶子节点的个数
3.XGBoost详细见xgboost的原理没你想像的那么难，通俗、有逻辑的写一篇说下Xgboost的原理，供讨论参考，下面简单列一下和GBDT的区别。
(1)将树模型的复杂度加入到正则项中，来避免过拟合，因此泛化性能会由于GBDT。
(2)损失函数是用泰勒展开式展开的，同时用到了一阶导和二阶导，可以加快优化速度。
(3)和GBDT只支持CART作为基分类器之外，还支持线性分类器，在使用线性分类器的时候可以使用L1，L2正则化。
(4)引进了特征子采样，像RandomForest那样，这种方法既能降低过拟合，还能减少计算
(5)在寻找最佳分割点时，考虑到传统的贪心算法效率较低，实现了一种近似贪心算法，用来加速和减小内存消耗，除此之外还考虑了稀疏数据集和缺失值的处理，对于特征的值有缺失的样本，XGBoost依然能自动找到其要分裂的方向
(6)XGBoost支持并行处理，XGBoost的并行不是在模型上的并行，而是在特征上的并行，将特征列排序后以block的形式存储在内存中，在后面的迭代中重复使用这个结构。这个block也使得并行化成为了可能，其次在进行节点分裂时，计算每个特征的增益，最终选择增益最大的那个特征去做分割，那么各个特征的增益计算就可以开多线程进行。
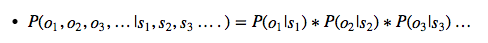
没有评论:
发表评论